Задачи про несуществующие треугольники
Известна задача из американского теста.
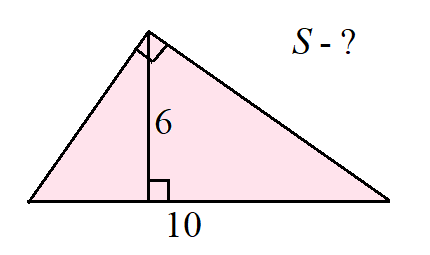
1. Найдите площадь прямоугольного треугольника, гипотенуза которого равна 10, а высота, проведённая к гипотенузе, равна 6.
Академик В.И. Арнольд рассказывал, что в США не сразу заметили, что учащиеся вычисляли площадь несуществующего треугольника (упомянутая высота не может быть больше половины гипотенузы).
Проколы бывают и в краю родных осин. Похожая ситуация случилась на сайте, где я нашёл такую задачу.
2. В треугольнике ABC провели медиану BM. Оказалось, что AB = MC = 7, а углы AMB и ACB равны соответственно 70 и 50 градусов. Найдите радиус окружности, описанной около треугольника ABC.
Готовимся к ОГЭ и ЕГЭ! Коварные задачи из экзаменационных вариантов!
Эту задачу полезно дать учащимся с заданием: докажите, что треугольник ABC, удовлетворяющий условиям задачи, не существует.
Доказательство. Угол AMB равен 70 градусов, из равенств АВ = МС = АМ следует, что угол АВМ равен 70 градусов. Угол С равен 50 градусов, тогда угол МВС равен 20 градусов, а угол АВС прямой. В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине. Тогда треугольник АВМ равносторонний, у него нет угла 70 градусов. Следовательно, треугольник ABC, удовлетворяющий условиям задачи, не существует, что и требовалось доказать.
Учащимся можно предложить найти другой способ доказательства. Вряд ли он будет короче решения, присланного Алексеем Владимировичем.
Если сторона AC треугольника в 2 раза больше стороны AB, то наибольшая величина угла С равна 30 градусам (если угол B прямой). Треугольник с углом C в 50 градусов не существует.