Задача про свечи. ВПР. 5 класс

Вспомнились строки Б. Пастернака.
Мело, мело по всей земле
Во все пределы.
Свеча горела на столе,
Свеча горела.
Это как защитная реакция после шока, который я испытал при чтении задачи для 5 класса. Читательница моего канала попросила: «Прокомментируйте, пожалуйста, задачу про горящие свечи из пособия Ященко за 5 класс. «Одновременно зажгли 3 свечи одинаковой длины, но разного диаметра». Как можно её решить, не составляя уравнения? Дети в шоке от этого пособия. Это обычная сош, нет у нас такого уровня подготовки».
Поискал я в Интернете. Поскольку я не в восторге от творчества коллектива И.В. Ященко, то не слежу за их новинками. Пропустил появление нового задачного сюжета для пятиклассников. Нашёл задачу. Позже выверил текст по книге [1].
1. Одновременно зажгли три свечи одинаковой длины, но разного диаметра. Длина каждой свечи 24 см. Первая свеча была самая толстая, вторая — потоньше, третья — самая тонкая. В тот момент, когда догорела третья свеча, первую и вторую тоже потушили. Оказалось, что огарок от первой свечи в два раза длиннее, чем от второй. За какое время полностью сгорает третья свеча, если известно, что первая сгорает за 6 ч, а вторая за 4 ч? [1]
«Ничего себе!» — Сказал я себе. Но почему в 5 классе? Ведь тот же авторский коллектив поддержал использование арифметических способов решения задач до применения уравнений. Они предлагали решения текстовых задач с помощью перебора, таблиц… Уже и в ЕГЭ включили задачи, решаемые арифметически…
Приведём авторское решение из книги [1].
Первая свеча горит со скоростью 24 : 6 = 4 сантиметра в час, вторая — со скоростью 24 : 4 = 6 сантиметров в час.
Пусть третья свеча сгорела за х ч. Тогда длина огарка первой свечи 24 – 4х (см), длина огарка второй свечи равна 24 – 6х (см).
24 – 4х = 2(24 – 6х ), откуда х = 3.
Это «взрослое» решение. Кажется, что «против лома нет приёма». А давайте поищем «детское» решение. Два первых действия оставим без изменения.
1) 24 : 6 = 4 (см/ч) — скорость сгорания первой свечи,
2) 24 : 4 = 6 (см/ч) — скорость сгорания второй свечи.
Давайте понаблюдаем за процессом горения свечей. Запишем в виде таблицы длину огарка каждой свечи через 1, 2…. часа. В правом столбце разделим первый результат на второй. Посмотрим, через сколько часов горения выполнится условие задачи.
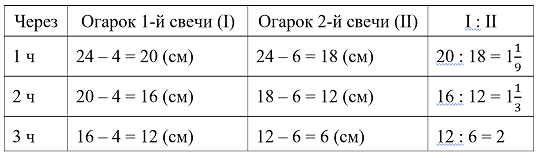
Как видно из таблицы, огарок первой свечи станет в 2 раза больше, чем огарок второй свечи, через 3 часа. Ещё через час вторая свеча догорит. Третья свеча горела 3 часа.
Ответ. 3 ч.
Развивая идею одного из комментаторов, покажем, что в задаче есть лишнее условие «24 см».
Через 1 час огарки свечей относятся как (1 — 1/6) : (1 — 1/4) < 2.
Через 2 часа огарки свечей относятся как (1 — 2/6) : (1 — 2/4) < 2.
Через 3 часа огарки свечей относятся как (1 — 3/6) : (1 — 3/4) = 2.
Дальнейшее увеличение времени горения (до 4 ч) делает отношение большим 2.
Для закрепления решите с детьми задачу из другого варианта. Только объясните им, что «полтора» это от старинного «пол втора», то есть «половина второго». Один с половиной.
2. Одновременно зажгли три свечи одинаковой длины, но разного диаметра. Длина каждой 16 см. Первая свеча была самая толстая, вторая потоньше, третья самая тонкая. Когда догорела третья свеча, первую и вторую потушили. Оказалось, что огарок первой свечи в полтора раза длиннее, чем от второй. За какое время сгорит третья свеча, если первая сгорает 8 ч., а вторая 4 ч? [1]
Ответ. 2 ч.
В Интернете есть разные «взрослые» способы решения задач такого типа. Есть приводящие к рациональному уравнению, которое в 5 классе, разумеется, не изучали.
Повторяю призыв из предыдущей моей статьи, посвящённой решению текстовых задач: «Уважаемые взрослые, не навязывайте детям свои взрослые мнения по поводу решения задачи. Сначала поищите возможное «детское» решение задачи».
Литература
1. Всероссийская проверочная работа. Математика : 25 вариантов. Типовые задания. ФГОС / Г.И. Вольфсон, Д.А. Мануйлов; под ред. И.В. Ященко. — М. : Издательство «Экзамен», 2020