Задача 25 из ОГЭ-2024. Произведение отрезков хорд

23.01.2024

Рассмотрим решение геометрической задачи из сборника [1]. Найти решение в ней не так просто.

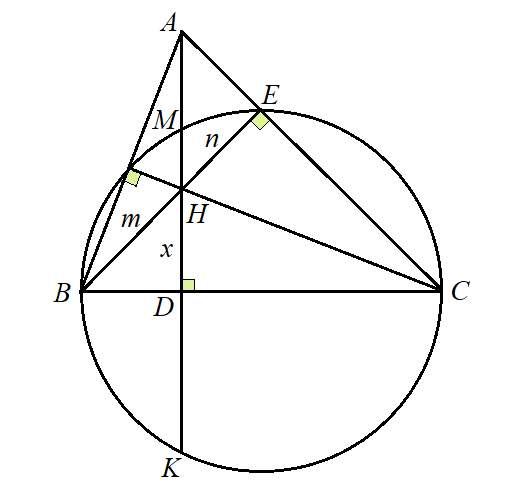
25. На стороне BC остроугольного треугольника ABC как на диаметре построена окружность, пересекающая высоту AD в точке M. AD = 80,
MD = 64, H — точка пересечения высот треугольника ABC. Найдите AH.

Решение. Введём обозначения: DH = x, BH = m, EH = n. Для нахождения AH найдём x, тогда 
AH = 80 – x.

Выразим mn через x другим способом. Для пересекающихся хорд BE и MK применим соответствующую теорему.

Так как MH = 64 – x, MD = KD = 64 — как отрезки хорды, перпендикулярной диаметру, KH = 64 + x, то mn = (64 – x)(64 + x).

Приравняем полученные результаты:

x(80 – x) = (64 – x)(64 + x).

Решив это уравнение, получим его единственный корень уравнения
x = 51,2. Тогда AH = 80 – x = 80 – 51,2 = 28,8.

Ответ. 28,8.

«Лишние» буквы m и n введены для краткости чтения отрезков, находить их значения не пришлось. Вместо них можно писать двухбуквенные обозначения отрезков.

Используемая литература

1. ЕГЭ. Математика. Профильный уровень : типовые экзаменационные варианты : 36 вариантов / под. Ред. И. В. Ященко. Москва : Издательство «Национальное образование», 2024.