Обобщение задачи на площади
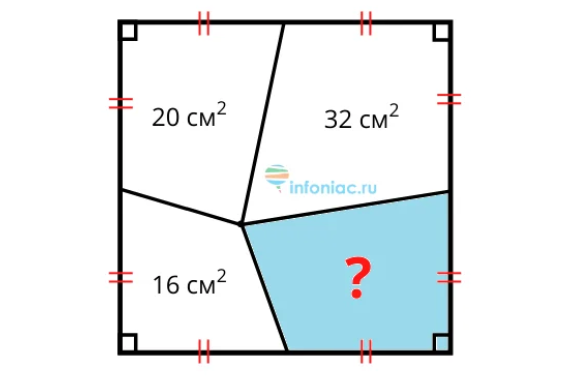
Встретилась в Интернете хорошая задача на площади.
1. Внутри квадрата дана точка. Её соединили отрезками с серединами сторон квадрата. Образовалось четыре четырёхугольника. Площади трёх из них заданы: 32, 20 и 16 (в квадратных сантиметрах) — см. рисунок выше. Найдите площадь четвёртого четырёхугольника.
Хорошая задача, сразу ясно, как её решать.
I способ. Соединим точку внутри квадрата ещё и с вершинами квадрата, применим мой любимый совет: «Не бойтесь вводить лишние буквы!» Обозначим площадь синего треугольника x (здесь и далее площади выражены в квадратных сантиметрах). Соседний с ним белый треугольник имеет ту же площадь (общая вершина, равные основания на одной прямой).
Далее, обходя квадрат против числовой стрелки, находим площади треугольников (они записаны рядом с каждой половиной стороны квадрата):
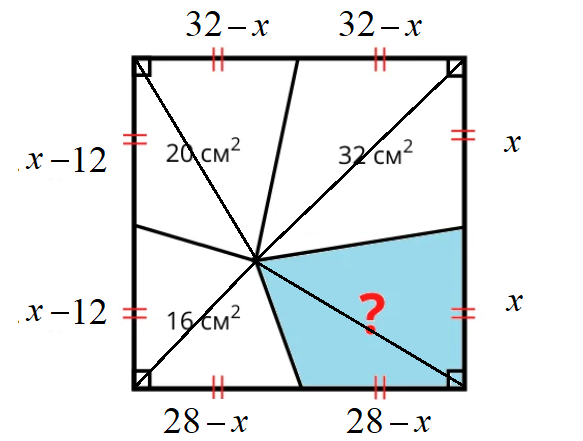
32 – x; 32 – x;
20 – (32 – x) = x – 12; x – 12;
16 – (x – 12) = 28 – x; 28 – x.
Второй синий треугольник имеет площадь 28 – x, а неизвестная площадь равна
28 – x + x = 28.
В комментариях после заметки нахожу своё решение и указание на более простое вычисление: 16 + 32 – 20 = 28. Давайте его обоснуем.
II способ. Рассмотрим две пары треугольников, которые получены при первом способе решения и имеют вершинами противоположные вершины квадратов. Розовым цветом закрасим пару треугольников, имеющих параллельные стороны, зелёным цветом — другую пару треугольников.
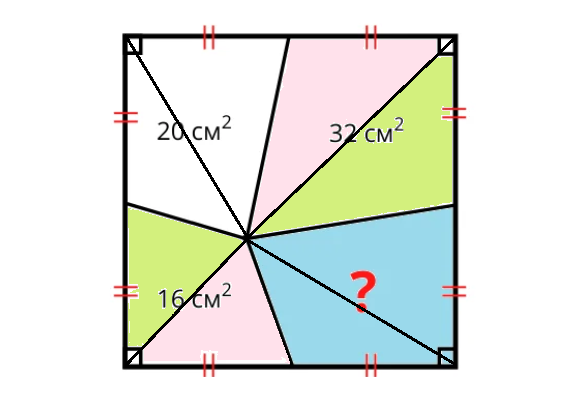
Сумма высот, проведённых к параллельным сторонам в розовых треугольниках, равна стороне квадрата, поэтому сумма площадей розовых треугольников равна 1/4 площади квадрата. Сумма площадей зелёных треугольников также равна 1/4 площади квадрата. А сумма площадей четырёх этих треугольников, равная 16 + 32 = 48, составляет 1/2 площади квадрата.
Сумма площадей оставшихся четырёх треугольников также равна 48, поэтому площадь синей фигуры равна 48 – 20 = 28.
Ответ. 28.
Давайте продлим удовольствие решать задачи на площадь. Изменим условия задачи.
2. Внутри прямоугольника дана точка. Её соединили отрезками с серединами сторон прямоугольника. Образовалось четыре четырёхугольника. Площади трёх из них заданы: a, b и c (в квадратных сантиметрах) — см. рисунок. Найдите площадь четвёртого четырёхугольника.
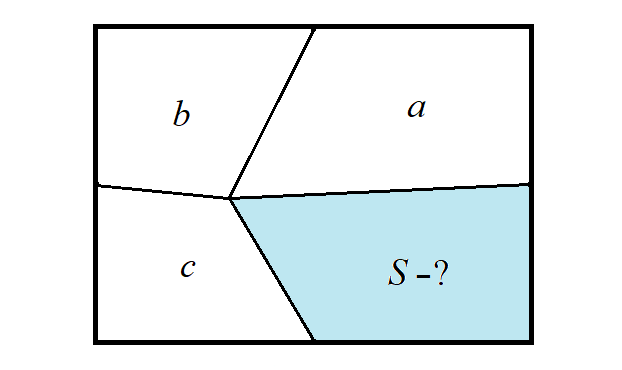
Убедитесь, что задача решается и первым, и вторым способом.
Ответ. a – b + c.
Продолжим обобщение первой задачи.
3. Внутри четырёхугольника дана точка. Её соединили отрезками с серединами сторон четырёхугольника. Образовалось четыре четырёхугольника. Площади трёх из них заданы: a, b и c (в квадратных сантиметрах) — см. рисунок. Найдите площадь четвёртого четырёхугольника.
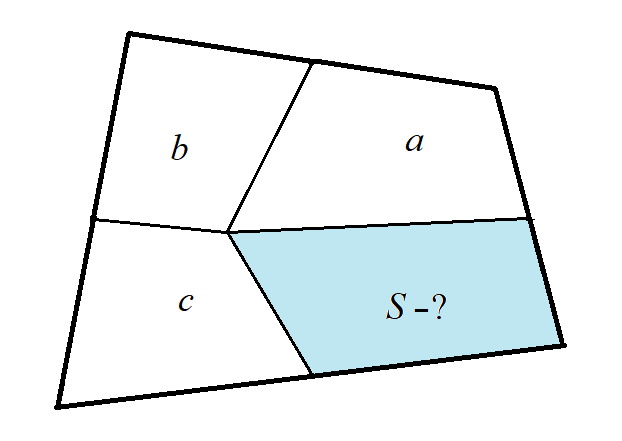
Убедитесь, что здесь применим лишь первый способ решения.
Ответ. a – b + c.
4. Внутри шестиугольника дана точка. Её соединили отрезками с серединами сторон шестиугольника. Образовалось шесть четырёхугольников. Площади пяти из них заданы: a, b, c, d и e (в квадратных сантиметрах) — см. рисунок. Найдите площадь шестого четырёхугольника.
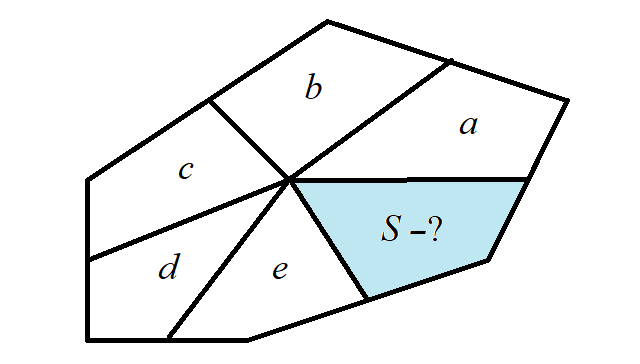
Ответ. a – b + c – d + e.
Задача обобщается на любое чётное число сторон многоугольника.
Хуже обстоят дела с аналогичной задачей для нечётного числа сторон многоугольника. Здесь не помогает ни первый способ решения, ни второй… Но из этого ещё ничего не следует. Поиски решения задачи про треугольник приводят к гипотезе, что эта задача не имеет решения.
В самом деле, если бы треугольник был задан своими элементами, по которым можно определить его площадь, то задача решалась бы легко. Но если треугольник не задан, то определить однозначно площадь третьего четырёхугольника невозможно.
Приведём пример. На рисунке изображены два прямоугольных треугольника, площади которых различны. Внутри них выбрано по точке и построены четырёхугольники. Площади двух из них 36 и 30. Площади третьих четырёхугольников различны.
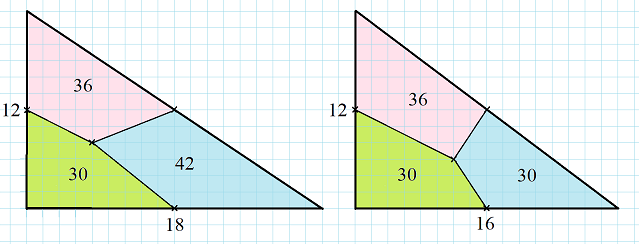
Заметка размещена в разделе Решайте с нами! Решайте, как мы! Решайте лучше нас! сайта www.shevkin.ru.
21.06.2020. Обобщение задачи на площади
Обсуждение заметки, замечания и предложения можно дать в комментариях на странице:
https://zen.yandex.ru/media/shevkin/obobscenie-zadachi-na-ploscadi-5eef97617b585908713e1fcf
Теги: задача на площади, математика, обучение