Две задачи про куб
Притомился я написанием трёх статей на тему войны и современной политики:
«Вот почему полмира обязаны России по гроб жизни»,
Войны США. Из истории «совести мира»,
Гитлер — проект англосаксов и Евросоюза 1930 годов.
Решил отдохнуть и придумал такую простую задачу.
1. Дан куб с ребром 1 (рис. а). На каждой его грани, как на основании построили правильную пирамиду с высотой 0,5 (рис. б). Получился новый многогранник. Сколько граней и каков объём этого многогранника?
Ответ. 12; 2.
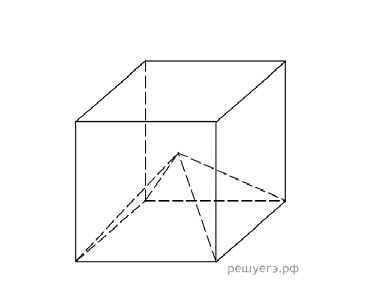
А наблюдательные решатели заметят, что если бы пирамиды строили не вне, а внутри куба, то все они имели бы общую вершину — центр куба. Каждая имела бы общие треугольные грани с четырьмя другими пирамидами (одна такая пирамида показана на рисунке к задаче 2). А все вместе они заполнили бы куб полностью. Поэтому сумма объёмов шести равных пирамид равна объёму куба и равна 1, тогда объем многогранника (рис в) равен 1 + 1 = 2. В этом втором случае мы обошлись без формулы объёма пирамиды.
2. (Задание 8. № 27184.) Объём куба равен 12. Найдите объём четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Надеюсь, объём пирамиды у вас получится легко.