Боря смог, или Снова про задачи на переливание из ЕГЭ
Про задачи на переливания я уже писал три раза, так как в сборниках для подготовки к ЕГЭ в задаче 19 (в) была неточность и ответ не соответствовал условиям задачи.
1) Задачи на переливания, или Алгоритм перебора всех случаев
2) Боря сможет, или Ещё раз про задания на переливания в ЕГЭ
3) Сколько моно? — Сколько нуно, столько и моно
Как говорится, вода и камень точит. Задачу 19 (в) переделали, разберём её решение.
19. У Бори нет источника воды, но есть три ведра различных объёмов, в двух из которых есть вода. За один шаг Боря переливает воду из ведра, в котором она есть, в другое ведро. Переливание заканчивается в тот момент, когда или первое ведро опустеет, или второе ведро наполнится. Выливать воду из вёдер запрещается.
а) Мог ли Боря через несколько шагов получить в одном из вёдер ровно 2 л воды, если сначала у него были ведра объёмами 4 л и 7 л полные воды, а также пустое ведро объёмом 8 л?
б) Мог ли Боря через несколько шагов получить равные объёмы воды во всех ведрах, если сначала у него были ведра объёмами 5 л и 7 л полные воды, а также пустое ведро объёмом 10 л?
в) Сначала у Боря были ведра объёмами 3 л и 6 л, полные воды, а также пустое ведро объёмом n л. Какое наибольшее натуральное значение может принимать n, если известно, что Боря сможет получить через несколько шагов ровно 4 л воды в одном из вёдер?
Источник. ЕГЭ 2021. Математика. Профильный уровень. 37 вариантов. Типовые варианты экзаменационных заданий от разработчиков ЕГЭ / Под ред. И.В. Ященко. – М.: Издательство «Экзамен», 2021.
Алгоритм перебора всех вариантов описан в статье, которую можно скачать. Там же есть условия и решения задач а) и б). Не будем повторяться.
Скачать: Задачи на переливания, или Алгоритм перебора всех случаев
Решение. в) Выполним алгоритм переливаний для n = 9. Запись «360» означает, что в исходном состоянии в первом ведре 3 л, во втором 6 л, в третьем 0 л воды. Зачёркнутая запись означает, что такое состояние было, дальнейшие переливания не нужны.
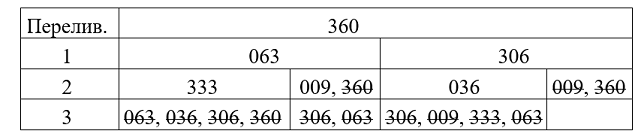
Получить 4 л воды в одном ведре невозможно, так как алгоритм переливаний завершен и 4 л не появилось ни в одном ведре. Кроме того, переливая объёмы, кратные 3, в вёдра, объёмы которых кратны 3, мы складываем и вычитаем числа, кратные 3, поэтому получить 4 л невозможно.
Если взять n > 9, то алгоритм переливаний полностью повторится, так как в третье ведро входит вся вода. Это означает, что для любого натурального n ≥ 9 Боря не сможет получить через несколько шагов ровно 4 л воды в одном из вёдер.
Выполним алгоритм переливаний для n = 8.

После получения записи 315 остановим алгоритм, так как следующим переливанием получим 045 — 4 л во втором ведре. Последовательность переливаний такова: 360 – 063 – 018 – 315 – 045. Наибольшее значение n равно 8.