Работа над ошибками. Логарифмическое уравнение

Всех ошибок не исправить,
Но к этому надо стремиться.
Прохожий.
Время от времени я пишу об ошибках, допущенных моими коллегами, блогерами, пишущими на тему математики. Не потому, что я идеален и не допускаю ошибок, допускаю. Небрежность вычислений и невнимательность достают и меня, но я благодарен судьбе, что есть внимательные читатели того, что я пишу, вовремя поправляют мои огрехи. Вот и я не могу пройти мимо явных ошибок, которые юные читатели могут дублировать на контрольных и экзаменах.
Итак, рассмотрим начало решения логарифмического уравнения.
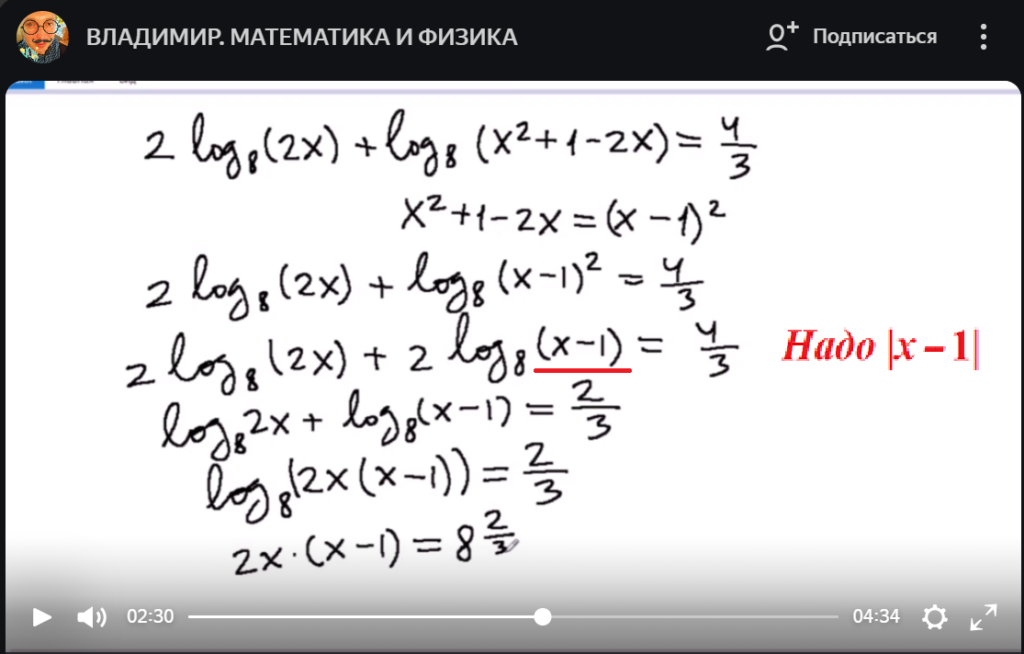
В третьем уравнении автор решения потерял знак модуля, как будто раскрыл его, считая, то x – 1 > 0.
Но x – 1 может быть отрицательным числом во втором уравнении, а в третьем уже только положительным? Покажем, как можно было решать это уравнение.

Блогер получил верный ответ при ошибочном ходе решения потому, что во втором случае, который он не рассматривал, уравнение не имело корней. Вот уравнение, специально составленное для того, чтобы показать, что неверный ход решения привёл бы к потере корней.

Теги: ЕГЭ, ЕГЭ математика Профиль, математика