Парадокс маляра, или Мы спорим о бесконечности

Довелось мне как-то давно возразить блогеру Виктору Буторову о бесконечных периодических десятичных дробях. Коллега когда-то критиковал наши учебники за «ошибки».
Например, за равенство 24,(9) = 25. Статью он назвал «В школу завезли образование Второй свежести». За учебники я спокоен. Они уже сами могут выбирать, кому нравиться, а кому нет. Но я возразил:
Виктор Буторов популяризирует безграмотность
В этой заметке я напомнил, что в России периодические десятичные дроби изучали ещё при царе-батюшке по учебнику А.П. Киселёва «Арифметика» с конца 19 века. И во всей нашей огромной стране не нашлось человека, возразившего тому, что такие дроби имеют отношение к реальной жизни. А Виктор Буторов возразил. Мои объяснения про то, что 1 = 0,(9) верно:
1 = 1/3 + 1/3 + 1/3 = 0,(3) + 0,(3) + 0,(3) = 0,(9)
не убедили «учителя математики» Виктора Буторова — вы понимаете, что я сильно сомневаюсь, что он учитель.
Под этой заметкой сегодня я обнаружил запись, оставленную другим блогером по имени Стив Май (псевдоним, как я понял), оставленную 12 дней назад.
Он поддержал моего критика в том отношении, что бесконечные периодические десятичные дроби не связаны с практикой и в качестве примера привёл парадокс маляра.
«Если взять квадратную пластинку 1 x 1 метр, потом приставить к ней ещё одну 0,5 x 1 м, а к той ещё одну 0,25 x 1 м, и так далее (каждый раз продлевая метровую сторону), то в конечном итоге выйдет бесконечно длинная пластинка с конечной площадью 1 + 1/2 + 1/4 + 1/8 +… = 2 м². Исходя из расхода краски 1 л на 5 м², нам понадобится всего 800 мл, чтобы без грунтовки покрасить эту пластину с двух сторон. Но поскольку длина её бесконечна, потребуется существенно больше — бесконечное количество краски».
Дальше у него идёт ненужная для нашего спора информация… Её пропускаю. Даю только вывод: «Число получается очень похожим на те самые 24,(9), о которых спорят Виктор и Александр. Но не то же самое. Да, Вы можете обучить учеников работать с бесконечными дробями. Можно даже компьютер/калькулятор этому обучить (вроде, в питоне и яве реализовано это равенство 1 – 1/3 – 1/3 – 1/3 = 0). Но это никогда не найдёт отражения в реальной жизни. 24,(9) у Вас всегда будет получаться либо немного больше 25, либо немного меньше, но «немного» не бесконечно, а очень даже недалеко от запятой…»
Человек, пишущий про математику, не верит математике, а верит своей интуиции, не зная, что интуиция иногда подводит? Для меня это удивительное открытие. Он пишет, что равенство 1 – 1/3 – 1/3 – 1/3 = 0 никогда не найдёт отражения в реальной жизни? Если я три раза из 1 м ленты вычту 1/3 м, то я не получу 0? Или получу его уже в нереальной жизни? О чём это Вы, коллега?
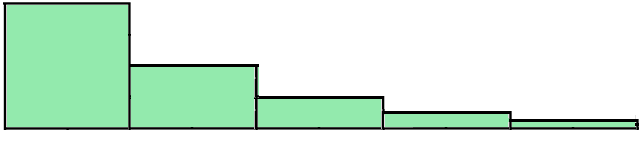
Итак, Стив Май рассказал нам о бесконечной последовательности пластинок
1 х 1; 1 х 1/2; 1 х 1/4; 1 х 1/8; 1 х 1/16; …
(на рисунке первые пять пластин) и сделал вывод о том, что нужно бесконечное количество краски.
Изобразим с увеличением в 2 раза (для большей наглядности) пластины той же площади, как показано на рисунке, и убедимся, что все они укладываются внутри двух квадратов 1 х 1:
1 х 1, 1/2 х 1, 1/2 х 1/2, 1/4 х 1/2, 1/4 х 1/4, …
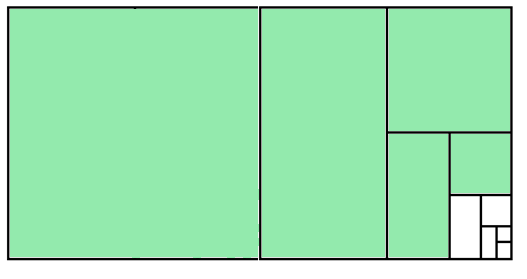
Закрашены 5 пластин, равновеликих пластинам на первом рисунке. Процесс закрашивания продолжается бесконечно долго, но никакого бесконечного количества краски не потребуется. Если маляру пора обедать, то пусть закрасит оставшийся не закрашенным квадрат 1/4 х 1/4 и идёт себе на обед. Краски надо ровно на 2 м² площади (с каждой стороны пластин), как и подсчитал Стив Май.
У Стива Мая есть продолжение: «Это ни в коей мере не возражение, это просто дополнение к Вашим словам о необходимости соглашений вроде 1 = 0,(9). Я вообще за то, чтобы такие вещи проходить на факультативах для интересующихся в старшей школе, а не на обычных уроках математики».
И тут я попал в ситуацию, которую описал анекдотом замечательный геометр И.Ф. Шарыгин, с которым мне посчастливилось работать в лаборатории обучения математике НИИ СиМО АПН СССР.
— Слушай, был вчера в Киеве и искупался в море…
— Ты с ума сошёл, там же нет моря!
— Вот чёрт, а я не знал и искупался.
Так и я. Ну не знал я мнения Стива Мая про факультатив и старшую школу и преподавал это ещё в далёком 1987/88 учебном году в школе № 679 города Москвы в своём первом авторском эксперименте, который только на днях вспоминал по другому поводу. В 5-м классе (теперь это 6-й класс). А дальше преподавал каждый раз в конце 6 класса и повторял чуть короче в начале 7 класса (современная нумерация классов).
И не нужно никакого соглашения там, где есть точное, а не приближённое равенство. Более того, надо бы знать детям в любом классе (про учителей математики и не говорю!), что если обыкновенная дробь несократима и в разложении её знаменателя на простые множители содержится хотя бы один множитель, отличный от 2 и 5, то эта дробь записывается в виде бесконечной периодической десятичной дроби. Мы этому учим в конце 6 класса.
Например, 1/3 = 0,(3); 17/99 = 0,(17); …
Надеюсь, мои оппоненты не будут возражать, что дроби 1/3, 17/99, … имеют некоторое отношение к практике и написанные мною равенства точные, а не приближённые. Можно проверить, разделив уголком числитель дроби на знаменатель… Другое дело, что при таком делении ещё никому не удавалось получить дробь с периодом 9, а равенство 24,(9) = 25 устанавливается иначе. Дроби с периодом 9 не используют, чтобы не было путаницы при поразрядном сравнении дробей. Всё это есть у нас в учебнике для 6 класса.
Стив Май убедил меня, что не надо из-за ковида отказываться от предложения одной московской школы провести урок для семиклассников с рассказом о действительных числах перед тем, как они начнут чертить непрерывные графики функций. Если получится провести, обязательно расскажу о том, как отреагировали самые обычные семиклассники на мой рассказ. Расскажу им и про парадокс маляра, за который Стиву Маю большое спасибо.
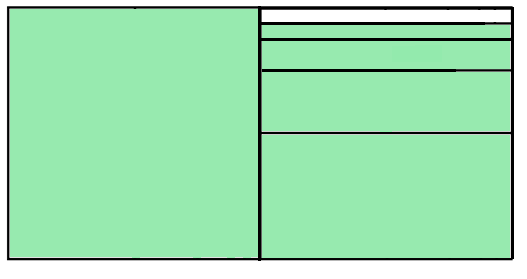
Дополнение от 11.03.2021. В комментариях подсказали более простой способ укладки пластин, чтобы не менять их формы. Спасибо. Закрашены те же первые 5 пластин, процесс закрашивания продолжается вечно, краска не выходит за пределы второго квадрата.
Теги: головоломки, ЕГЭ по математике, математика, ОГЭ по математике